Giorgio Vasari (1511-1575) was een Italiaans schilder en architect. Hij werd vooral bekend als schrijver van het boek 'Le Vite de piu eccellenti Architetti, Pittori e Scultori' dat in 1550 verscheen. Dit werk is een verzameling levensbeschrijvingen van kunstenaars vanaf Giotto toi Michelangelo, de leermeester van Uasari. De beschrijvingen zijn voornamelijk gebaseerd op eigen waarnemingen en mondelinge overleveringen. De betrouwbaarheid is hierdoor niet altijd even groot.
Het boek geeft wel een prachtig inzicht in de toenmalige opvattingen en ideeën over kunst.

Het leven van Leon Battista Alberti, Florentijns architect, 1404-72.

Niets is zo vruchtbaar als het samenvallen van theorie en praktijk, omdat artistieke vaardigheden versterkt en geperfectioneerd worden door de wetenschap. De goede raad en geschriften van onderlegde kunstenaars leggen meer gewicht in de schaal en hebben meer effect dan de woorden of het werk van hen die (ongeacht de kwaliteit) voornamelijk mensen van de praktijk zijn.

Dat deze opmerkingen steek houden wordt duidelijk aangetoond door Leon Battista Alberti. Hij wijdde zich aan de studie van het latijn en de praktijk van de bouwkunst, het perspectief en de schilderkunst en hij liet het nageslacht een paar boeken na van zijn hand. Nu heeft geen van onze hedendaagse vaklieden geweten hoe hij over deze dingen moest schrijven en, ook al hebben velen van hen betere dingen gemaakt dan Alberti, de invloed van zijn geschriften op de pennen en redevoeringen van geletterde mensen is van dien aard geweest, dat men hem gewoonlijk superieur acht aan hen die in feite beter waren dan hij. Dus we zien dat voor zover het roem en reputatie betreft, het geschreven woord langer voortbestaat en invloedrijker is dan wat dan ook. Want als ze oprecht zijn en geen leugens bevatten, gaan boeken gemakkelijk van hand tot hand en er wordt alom geloof aan gehecht. Het is daarom niet verwonderlijk dat de beroemde Leon Battista Alberti bekender is door zijn geschriften dan door wat hij maakte.

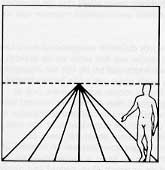
Alberti en Brunelleschi hebben de wetmatigheden in de perspectief niet ontdekt, want veel verschijnselen waren al bekend. Wel hebben ze de kennis in een logische samenhang gebracht.
Alberti's bijdrage aan de perspectief als wetenschap is opgetekend in zijn tractaat 'De Pittura' uit 1435. De 'costruzione legittima' of wel de 'beste methode' zoals hij het zelf noemde, beschrijft wetenschappelijk de constructie van een schaakbord of tegelvloer in perspectief. Tot dan toe was het gebruikelijk om de grootte van vierkanten in een tegelvloer steeds met een derde te verminderen.

Alberti's methode berust op het volgende principe: In fig. 1 is het beeldvlak (tafereel) verticaal geplaatst. De grondlijn valt samen met de eerste naad van een horizontale tegelvloer. Loodrecht op het beeldvlak of tafereel is een ander verticaal vlak geplaatst waarin de punten V (verdwijn- of vluchtpunt) en O (oogpunt van de beschouwer) liggen. De gezichtskegel die bestaat uit de bundel lijnen die van de tegelvloer naar het oog O lopen wordt doorsneden door het beeldvlak. Deze doorsnede vormt het perspectief van de tegelvloer. De orthogonalen (de lijnen die loodrecht op het beeldvlak staan) moeten elkaar noodzakelijkerwijs snijden in V (verdwijnpunt)

In fig. 2 is het verticale vlak dat door V en O gaat omgeklapt in het beeldvlak. Het punt O heet nu D (distantiepuntJ waarmee de afstand van het oog tot het beeldvlak wordt aangegeven. De lijnen die de lichtstralen naar het oog (projectielijnen) voorstellen vallen nu samen met de diagonalen van de vierkanten waaruit blijkt dat de afstand van het verdwijnpunt naar het oog even groot is als de afstand van het verdwijnpunt naar het distantiepunt. Alberti geeft hiermee de wetenschappelijke verklaring voor de distantiepunt methode' die Brunelleschi al gebruikte in zijn schildering van het Baptisterium.

Zijn uiteenzetting is niet overal duidelijk. Alberti was zich daar ook van bewust want hij verontschuldigt zich hiervoor en wijt het aan de nieuwigheid van de materie en aan de beknoptheid van zijn commentaar.

Allereerst een opmerking over het kader, waarbinnen ik teken. Ik maak een rechthoek, zo groot als ik wil, die ik beschouw als een open venster waardoorheen ik zie wat ik wil schilderen.
Hier bepaal ik naar believen de afmetingen van de personen in mijn schilderij. Ik verdeel de lengte van deze persoon in drie delen. Deze delen staan voor mij in verhouding tot de maat die 'braccio' (el) heet, want als men het na meet blijkt, dat de gemiddelde man drie el groot is. Met deze 'el' verdeel ik de basislijn van de rechthoek in zoveel delen als mogelijk is. Voor mij is deze grondlijn van de rechthoek proportioneel met de dichtstbijzijnde dwarslijn (transversaal) en van gelijke afstand op de tegelvloer.
Vervolgens kies ik een punt binnen deze rechthoek, waar het mij het beste lijkt, waarop de centrale straal valt (het verdwijnpunt). Daarom wordt dit het 'centrale punt' genoemd. Het punt is juist gekozen als het niet hoger boven de basislijn van het vierkant ligt dan de hoogte van de man die ik daar zou willen schilderen. Zodoende lijken zowel de beschouwer als de geschilderde dingen zich op het zelfde vlak te bevinden. Als het centrale punt eenmaal zo is vastgelegd, trek ik rechte lijnen hiervandaan naar iedere verdeling op de grondlijn van de rechthoek. Deze getrokken lijnen, verlengd tot in het oneindige, laten mij zien hoe iedere maat voor het oog verkleind wordt. Sommigen trekken gewoonlijk hier een dwarslijn evenwijdig aan de basis van de rechthoek. De afstand tussen die twee lijnen verdelen ze dan in drieën en trekken dan op tweederde een nieuwe lijn. Zo trekken ze steeds nieuwe lijnen op dezelfde manier zodat de in derden verdeelde ruimte tussen de eerste en tweede steeds in een vaste verhouding zich uitbreidt. Op deze manier voortgaande zouden de tussenruimtes, zoals de wiskundigen zeggen, 'superbipartienti' zijn aan de volgende tussenruimtes. Ik kan wel vertellen dat zij, die dit gewoonlijk doen, zich vergissen, ook al volgen ze de correcte manier van schilderen bij andere dingen. Want als de eerste lijn lukraak geplaatst is, zelfs als de andere er logisch uit volgen, kan men nooit met zekerheid zeggen waar de top van de gezichtskegel ligt. Hierdoor ontstaan heel wat tamelijk grote fouten in de schilderkunst.
Voeg daar nog eens bij hoezeer deze schilders dwalen als ze het centrale punt hoger of lager plaatsen dan de hoogte van de geschilderde mensen. Bedenk dat een geschilderd ding nooit waarheidsgetrouw kan lijken als de afstand waarop het bekeken moet worden, niet vast ligt.( ...)

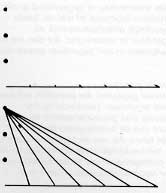
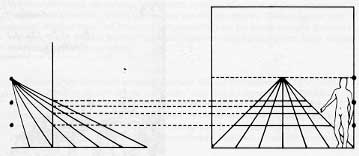
Laten we terug keren naar ons onderwerp. Ik vind deze methode de beste. Doe alles zoals ik gezegd heb, kies het centrale punt, trek de lijnen hiervandaan naar de verdeling op de grondlijn van de rechthoek. Bij de afstanden tussen de horizontale lijnen, die steeds verder weg liggen, doe ik als volgt: Op een aparte plek trek ik een rechte lijn die ik verdeel in dezelfde delen waarin ik de grondlijn van de rechthoek verdeeld heb. Vervolgens zet ik een punt op dezelfde hoogte als het centrale punt ten opzichte van de grondlijn. Ik trek lijnen van dit punt naar iedere verdeling op de eerste lijn. Vervolgens stel ik naar believen de distantie (afstand) van het oog tot het schilderij vast. Hier trek ik, zoals de wiskundigen zeggen, een verticaal die deze lijn doorsnijdt. Een verticaal is een rechte lijn die als hij een andere rechte lijn snijdt, er ook rechte hoeken mee maakt. De snijpunten van deze verticaal met de andere lijnen geeft mij de opeenvolgende afstanden van de dwarslijnen. Op deze manier vind ik alle evenwijdige lijnen, dat wil zeggen, de maten (el) in het vierkant van de tegels in het schilderij. Als de diagonalen van verschillende vierkanten op het schilderij op één rechte lijn liggen, is dat een aanwijzing voor mij dat ze juist getekend zijn.